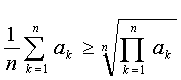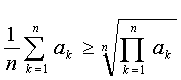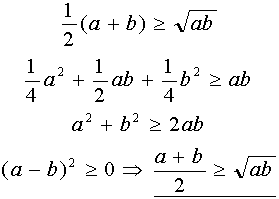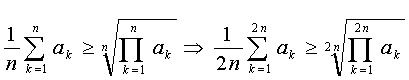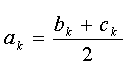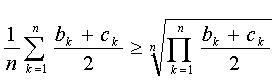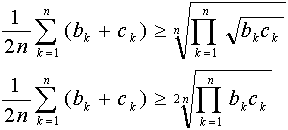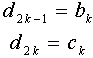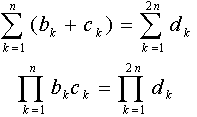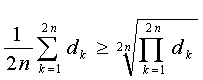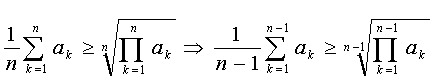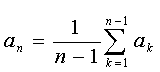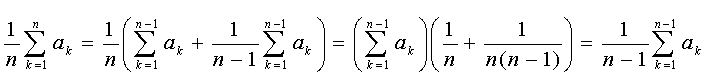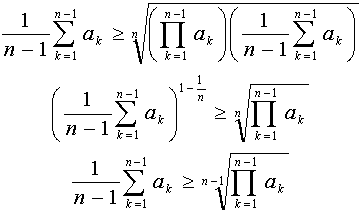
Důkaz AG nerovnosti
Tahle stránka je zajímavá ze dvou důvodů. Nejenom, že znalost této věty se může hodit, ale v inkriminovaném důkaze je takové množství "vychytávek", že je užitečné si ho alespoň přečíst. Mimochodem je to můj první dvoustránkový důkaz na MFF. Takže se do toho pusťme:
AG nerovností nazýváme větu o tom, že aritmetický průměr je vždy větší nebo roven průměru geometrickému. Chceme tedy dokázat, že pro jakoukoli konečnou posloupnost nezáporných (!) reálných čísel platí:
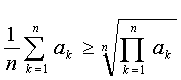
Pro n=1 je důkaz triviální. V pozdějších úvahách použijeme i poznatek, že tato nerovnost platí i pro n=2. Tedy
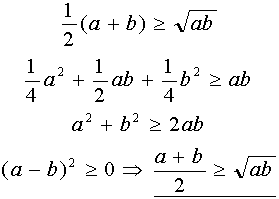
Použijeme nestandardní způsob důkazu matematickou indukcí. Máme již důkaz pro n=1 (krok 1). Teď dokážeme, že pokud nerovnost platí pro nějaké obecné n, pak platí i pro 2n (krok 2). Později pak dokážeme, že pokud nerovnost platí pro n, pak platí i pro n-1 (krok 3). Tím bude důkaz hotov. Nyní máme tedy dokázat implikaci (1)
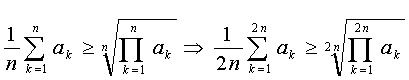
Libovolné reálné číslo lze vyjádřit jako aritmetický průměr dvou jiných (blíže neurčených). Můžeme tedy definovat členy vstupní posloupnosti takto:
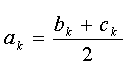Výraz na levé straně implikace (1) teď přepíšeme do tvaru
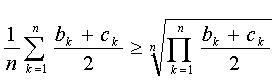
Máme-li dokázán poznatek, že AG nerovnost platí pro n=2, můžeme s využitím tranzitivity nerovností upravit pravou stranu takto
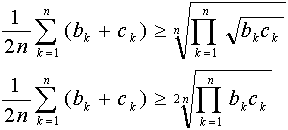
Uvažujme nyní posloupnost dk, definovanou následovně
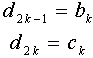
Potom platí vztahy
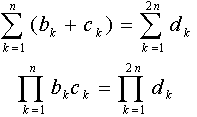
Získanou nerovnost můžeme tedy zapsat ve tvaru
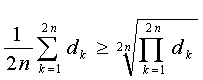
Což je přesně AG nerovnost pro 2n. Implikace (1) tedy platí. Posledním krokem důkazu je důkaz implikace (2). Tedy
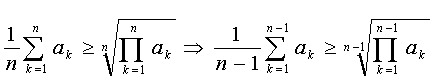
Směrem zleva doprava vlastně z posloupnosti ubíráme poslední člen. Proto můžeme v předpokladu implikace dosadit za poslední člen posloupnosti pevné číslo. Pro náš důkaz si tedy zvolíme aritmetický průměr všech předchozích členů. Neboli
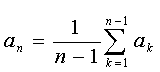
Po dosazení následuje několik úprav,
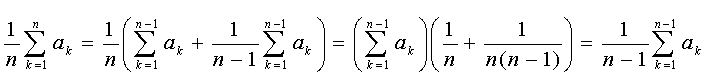
z nichž je patrný důvod volby an. Můžeme tedy psát
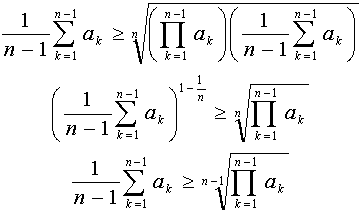
Obdrželi jsme AG nerovnost pro n-1. Tím je důkaz proveden pro libovolnou vstupní posloupnost.
Special thanx goes to Luboš Pick. Všechny vzorce z téhle stránky jsou zazipované tady.
Pokud se vám něco nezdá, pošlete e-mail autorovi stránky.
Můžete se vrátit zpět na homepage anebo tam, odkud jste přišli.
