Důkaz Pythagorovy věty
Maďarský matematik Georg Pólya je známý svým přístupem k matematickým důkazům. Trik spočívá v tom, že problém rozšíříme na třídu ekvivalentních problémů a z nich vyřešíme ten nejjednodušší. Může se zdát, že to k žádnému zjednodušení nevede, ale podívejte se na následující příklad. Dokážeme si notoricky známou větu Pythagorovu, která říká, že součet obsahů čtverců nad odvěsnami pravoúhlého trojúhelníka je roven obsahu čtverce nad přeponou.
Po vzoru Pólyi si ji nejdříve zobecníme. Proč by měla platit jenom pro čtverce? Když do čtverce nakreslíme nějaký jiný útvar - kruh, půlkruh, trojúhelník nebo cokoli jiného, bude poměr obsahů tohoto útvaru a čtverce zachován při zvětšování a zmenšování měřítka. Označme tento poměr k. Dále si uvědomíme, že tvrzení
a2 + b2 = c2
je ekvivalentní tvrzení
a2k + b2k = c2k.
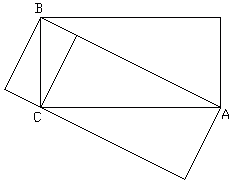
Takže Pythagorova věta by měla platit nejen pro čtverce, ale pro libovolné geometricky podobné útvary, jejichž lineární rozměry odpovídají stranám pravoúhlého trojúhelníka. Ze všech takových útvarů si vybereme pravoúhlé trojúhelníky naznačené na obrázku.
Když do trojúhelníka ABC přikreslíme výšku na přeponu, vidíme okamžitě, že součet obsahů trojúhelníků nad odvěsnami je roven obsahu trojúhelníka nad přeponou. A tím je dokázána i Pythagorova věta.
Takový důkaz je nejen krásně přehledný, ale navíc dokazuje mnohem silnější tvrzení.
Special thanx goes to Roman Tomášek. Připomínky posílejte mailem na adresu egg@matfyz.cz.
Můžete se vrátit na hlavní stránku nebo tam, odkud jste přišli.
