 Zajímavé topologické útvary
Zajímavé topologické útvary
Matematikové studující topologii a teorii grafů objevili podivuhodné vlastnosti, které vykazují některé geometrické útvary.
Möbiův list
Möbiův list (někdy též proužek, páska atd.) nese jméno matematika a fyzika z 19. století A. F. Möbia. Vezměme proužek papíru ve tvaru úzkého obdélníka. Dva konce proužku slepíme tak, že jeden pootočíme oproti druhému o 180o. Vzniklý útvar se jmenuje Möbiův list.
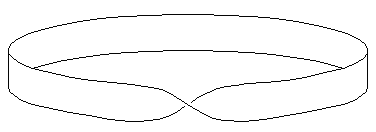
Möbiův list
Obyčejný papír má dvě strany, řekněme rub a líc. Jenže na Möbiově listě rub a líc neodlišíme. Můžeme třeba jednu stranu papíru obarvit zeleně a druhou červeně. Ale když začnete v nějakém místě barvit Möbiův proužek, obarvíte jej nakonec celý. Möbiův list má jen jeden povrch.
Na první pohled má tento útvar dva okraje. Ale když si zkusíte jet prstem po jeho okraji, poznáte, že zdání klame. Okraj je jediná uzavřená křivka.
Na původním papíře jsme také mohli zavést souřadný systém. Každý bod na obyčejném papíru můžeme jednoznačně popsat dvěma souřadnicemi. Ale na Möbiově litu se nám to překvapivě nepodaří. Nedá se vymyslet jednoznačné přiřazení mezi body na povrchu a souřadnicemi. Matematikové cizím slovem říkají, že plocha Möbiova listu není parametrizovatelná.
A teď si zkuste představit, že jste dvourozměrná bytost a že žijete na Möbiově proužku. Nemůžete z něj ven, ten proužek je pro vás celým vesmírem. A v takovém vesmíru se dějí divné věci. Můžete jít pořád rovně a vrátíte se do výchozího bodu. To se ještě dá pochopit. Víme, že třeba mořeplavcům se podobná věc stává, když plují kolem Země. Ale když proužek opravdu obejdete, najednou si uvědomíte, že jste nějak obráceně! Věci, které jste před cestou měli po levé ruce, jsou teď vpravo. Zkusíte se otočit a všelijak se vrtíte a kroutíte, ale to nepomáhá. Teprve když znovu obejdete celý list dokola, je všechno jako dřív.
Kleinova láhev

Kleinova láhev
Kleinova láhev neohraničuje žádný prostor, jak se na první pohled zdá. Nemůžeme rozhodnout, který bod prostoru je "venku" a který "uvnitř". Další zvláštností je, že tato plocha má jen jeden povrch, stejně jako Möbiův list. Nemůžeme si ji ale tak snadno vymodelovat, protože papír by musel protínat sám sebe...
Hyperkrychle
Hyperkrychle mají i praktické využití; například jako tvar počítačové sítě. Matfyzákovi poslouží hlavně k procvičení n-rozměrného myšlení.
Definice je induktivní. 0-rozměrná krychle je jeden bod. A máme-li už n-rozměrnou krychli, sestrojíme z ní (n+1)-rozměrnou tak, že vytvoříme dvě její kopie a odpovídající body na nich spojíme úsečkou. Takže 1-rozměrná krychle je úsečka, 2-rozměrná krychle je čtverec, 3-rozměrná je normální krychle. Od vyšších čísel už speciální názvy nemáme a mluvíme o n-rozměrné hyperkrychli.
Představa hyperkrychle jako geometrického tělesa je názorná, ale u vyšších dimenzí taková intuice selhává. Naštěstí si ale můžeme krychli představovat jako graf. Graf je množina vrcholů, z nichž některé jsou spojeny hranami. Vrcholy si můžeme představit jako puntíky a hrany jako úsečky mezi nimi. Tak znázorňuje hyperkrychle i náš obrázek.

Hyperkrychle různých dimenzí
A ještě jinak můžeme vyjádřit hyperkrychli. Za vrcholy n-rozměrné krychle budeme považovat všechny n-prvkové posloupnosti nul a jedniček. Hrana mezi dvěma vrcholy vede právě tehdy, když se posloupnosti liší v jediné číslici.
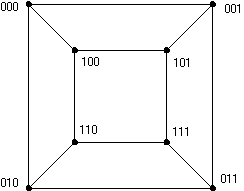
Kabelem propojíme ty počítače, jejichž adresy se liší v jedné číslici
Je zřejmé, že n-rozměrná krychle má 2n vrcholů, protože 0-rozměrná má jeden a každá další dvakrát víc než předchozí. Zkuste si pro zajímavost spočítat, kolik má která hyperkrychle hran a kolik stěn. Všimněte si při tom, že to, co je pro 3D krychli objemem, je pro 4-rozměrnou jen "povrch". Stejně jako plocha čtverce odpovídá povrchu krychle, stejně jako délka úsečky odpovídá obvodu čtverce.
Připomínky a dotazy posílejte mailem na adresu egg@matfyz.cz.
Můžete se vrátit zpět na homepage anebo tam, odkud jste přišli.

 Zajímavé topologické útvary
Zajímavé topologické útvary Zajímavé topologické útvary
Zajímavé topologické útvary


