Fraktální geometrie a počítačová grafika - principy a algoritmy
Základy fraktální geometrie položil před více než třiceti lety matematik B. B. Mandelbrot. On sám ji označil za morfologii amorfního. Nezávisle na ní vznikla zhruba v téže době teorie tzv. deterministického chaosu. V podstatě se nezávisle na různých místech vytvořilo nové téma ve vědě: hledání řádu v chaosu.
Klasická euklidovská geometrie se zabývá studiem ideálních pravidelných útvarů jako čtverce, kružnice, pravidelné mnohoúhelníky a mnohostěny. Naproti tomu fraktální geometrie studuje tvary tak členité jako třeba hory, pobřeží, mraky, elektrické výboje, stromy, špinavé skvrny a podobně. Odtud plyne její praktické využití v počítačové grafice a simulaci.
Budeme studovat vlastně limity posloupností množin, které se vyznačují opakováním téhož vzoru ve stále menším měřítku. Vlastnost být invariantní vůči změně měřítka nazval Mandelbrot soběpodobnost (self-similarity). K "měření" takových útvarů již nelze použít prostředky klasické geometrie. Proto se jako míra členitosti definuje tzv. Hausdorfova dimenze. Její definice je složitá, ale pro dosti velkou třídu soběpodobných množin lze Hausdorfovu dimenzi spočítat podle jednoduchého vzorce. V případě, že námi zkoumaný objekt obsahuje n kopií sebe sama zmenšených na jednu k-tinu je Hausdorfova dimenze rovna log(n) / log(k). Lépe to ukážeme na příkladu.
Jedním z nejjednodušších fraktálních útvarů je Cantorovo diskontinuum. Začneme s úsečkou libovolně zvolené délky. Tu rozdělíme na třetiny a prostřední část smažeme. Získáme tak dvě úsečky, s nimiž postup opakujeme. Kdybychom totéž opakovali až donekonečna, získali bychom množinu nekonečně mnoha bodů, jejichž celková délka by byla 0. To je Cantorovo diskontinuum. Všimněme si nyní, že taková množina obsahuje dvě kopie sebe sama zmenšené na třetinu. Hausdorfova dimenze Cantorova diskontinua je tedy log 2 / log 3 = 0.6309...
Prvních šest aproximací Cantorova diskontinua
Pojem Hausdorfovy dimenze použil Mandelbrot pro exaktní definici soběpodobné množiny, kterou nazval fraktál. Je to taková podmnožina euklidovského prostoru, pro niž je Haudorfova dimenze ostře větší než dimenze topologická (viz níže). Hladké křivky mají Hausdorfovu dimenzi rovnou 1, avšak s rostoucí členitostí tato dimenze roste. Dokonce existují křivky, jejichž Hausdorfova dimenze je rovna 2. Podobně dvojrozměrné útvary s Hausdorfovou dimenzí větší než 2 jsou fraktály.
Soběpodobné obrazce se dají velice dobře aproximovat počítačem. Opakování téhož vzoru se přirozeně realizuje voláním téhož podprogramu se stále zmenšujícími se parametry. Pokud do těchto algoritmů zavedeme náhodný prvek dostaneme takzvané statisticky soběpodobné fraktály. Například v Cantorově diskontinuu nebudeme úsečky dělit na třetiny, ale zvolíme náhodně dva body. Pomocí takovýchto algoritmů se dají velmi dobře simulovat mnohé přírodní útvary. Krása statisticky soběpodobných fraktálů spočívá v křehké harmonii mezi pravidelností a nahodilostí. Stejně jako krása přírody. V lese nepanuje chaos, přestože je každý strom jedinečný. Proto se nám les zdá krásnější než sídliště se svojí umělou pravidelností i než smetiště, které je úplně chaotické.
Při studiu množin invariantních vůči nelineárním transformacím objevil Mandelbrot nepřeberné množství krásných a zajímavých fraktálů. Nejjednodušší třídou jsou Juliovy množiny, které si nyní blíže popíšeme. Nejjednodušší nelineární racionální komplexní funkce je kvadratický polynom fc (z) = z 2+ c, kde c je komplexní parametr. Juliova množina této funkce je hranice množiny těch z, pro která je posloupnost { fc(z), fc fc(z)=fc2, ... }, vytvořená postupným iterováním této funkce, omezená. Svět tvarů Juliových množin je neočekávaně bohatý. S výjimkou c=0 (jednotková kružnice) a c=-2 (reálný interval <-2, 2>) jsou Juliovy množiny soběpodobné fraktální množiny nejrůznějších tvarů. Pokud bodům obrazovky přiřadíme komplexní čísla analogicky jako v Gaussově rovině, můžeme určit barvu podle rychlosti divergence iterací. Tak získáme překvapivě estetické obrazy, které je možné dále využít v počítačové grafice.
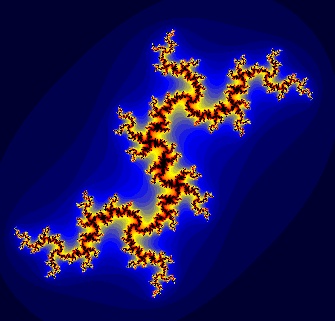
Takhle vypadá Juliova množina pro c = -0.76i
Další zajímavé tvary Juliových množin na vás čekají tady.
Klíčem ke klasifikaci chování funkcí fc (z) = z 2 + c v závislosti na parametru c je tzv. Mandelbrotova množina. Je to množina takových c, pro která je Juliova množina funkce fc (z) souvislá. P. Fatou a G. Julia ukázali, že množina je souvislá právě když je posloupnost { c, c2+ c, (c2+ c)2+ c, ... } omezená. Topologická dimenze Juliových množin závisí na poloze parametru c vzhledem k Mandelbrotově množině M: Je-li c uvnitř M, pak je topologická dimenze rovna 2, je-li c na hranici M, pak je dimenze 1 a je-li c mimo M je topologická dimenze rovna 0. Dlužno dodat, co je to topologická dimenze. Tenhle exaktní pojem de facto odpovídá intuitivnímu pojmu rozměr. Křivky jsou jednorozměrné, plošné útvary dvojrozměrné, prostorové trojrozměrné apod. Množiny bodů rozmístěných nesouvisle mají topologickou dimenzi 0.
Mandelbrotova množina je zřejmě nejznámější fraktální útvar.
Klepnutím na obrázek zobrazíte BMP verzi o velikosti 225kb. Klepnutím sem si můžete stáhnout moje zdrojáky v Borland Pascalu pro DOS. Jsou to dva programy, které generují Juliovy množiny a Mandelbrotovu množinu. Unita rat.tpu slouží k základnímu ovládání myši. Její zdroják mi zničily Windows, ale použití těch rutin je intuitivní. Komentáře píšu v angličtině, doufám, že to nikomu nevadí. Připojil jsem i podrobnou dokumentaci v češtině jako .txt bez diakritiky.
Pro obecnou komplexní racionální funkci mají všechny oblasti přitažlivosti společnou hranici, na níž je dynamika chaotická. Pěkným příkladem takové funkce je f(z) = ( 2z 3 + 1) / 3z 2,
pomocí níž lze takzvanou Newtonovou iterační metodou najít kořeny rovnice z 3 - 1 = 0.
Tento dynamický systém má tři jednobodové atraktory (kořeny zmíněné rovnice). V oblasti přitažlivosti každého z těchto tří atraktorů je Newtonova metoda účinná, neboť vyjdeme-li z libovolného bodu oblasti, dostaneme postupným iterováním funkce ( 2z 3 + 1) / 3z 2 posloupnost konvergující k příslušnému kořenu rovnice. Tyto tři oblasti mají společnou hranici, Juliovu množinu funkce ( 2z 3 + 1) / 3z 2, na níž je Newtonova metoda neúčinná. Tato hranice je zajímavě členitá fraktální množina s chaotickou dynamikou.
Newtonova metoda řešení rovnice z 3 - 1 = 0.
Tři oblasti přitažlivosti jsou barevně rozlišeny, jasnost barvy naznačuje rychlost konvergence. Opět dávám k dispozici svůj zdrojový text v Pascalu. Jako shrnutí následuje návod, jak si vytvořit vlastní fraktál - Juliovu množinu.
Vezměte jakoukoli racionální komplexní funkci, která vás napadne. Iterování se provádí následovně: vyjděte z nějakého komplexního čísla, dosaďte do vaší funkce a výsledek opět použijte jako vstup. Zjistěte jakoukoli metodou (třeba i pokus-omyl) některý z atraktorů posloupnosti vzniklé iterováním. Pak už stačí měřit, jak rychle posloupnost konverguje k tomuto atraktoru (diverguje). Pokud je atraktor nekonečno, obvykle stačí měřit po kolika iteracích přesáhne člen posloupnosti určitou absolutní hodnotu. Pokud je jednobodový, stačí si zvolit konstantu epsilon a zjišťovat, po kolika iteracích se přiblížíme na epsilonovou vzdálenost (přesnost). Každému pixelu přirozeným způsobem přiřadíte komplexní číslo (Gaussova rovina). To je výchozí bod pro iterování. Barva tohoto pixelu bude odpovídat zjištěné rychlosti konvergence.
Pokud vás fraktální grafika zajímá a chcete vidět na vlastní oči, co dokáže, podívejte se na tohle!
Máte-li dojem, že v textu chybí některé definice, máte pravdu. Na požádání vám je dodám, ale pro rámec tohoto článku se mi zdály příliš složité.
Při programování se vám bude hodit unita mode101h.pas.
Linx: The Mandelbrot Set and Julia Sets, Jemný úvod do fraktálů
Zdrojem informací mi byl především časopis Pokroky matematiky, fyziky a astronomie, ročník 34 (1989), číslo 5.
Připomínky posílejte autorovi stránky. Můžete se vrátit zpět na homepage anebo tam, odkud jste přišli.
